

Next:Comparando
Com Outras CurvasUp:O
Problema da BraquistócronaPrevious:Refração
na Atmosfera Terrestre
De Volta à Braquistócrona
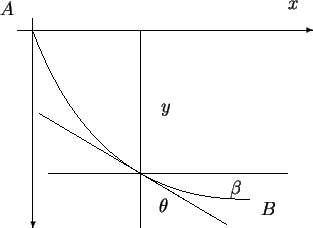
Para finalizar o problema da braquistócrona consideremos a figura
abaixo
|
Figura 7: Buscando uma equação
para o problema.
Como a partícula tem de descrever a trajetória mais rápida
e sua velocidade escalar é variável (lembre-se que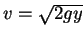 ),
tudo se passa como no caso do raio de luz que atravessa um meio não-homogêneo.
Assim, pela seção anterior, devemos ter
),
tudo se passa como no caso do raio de luz que atravessa um meio não-homogêneo.
Assim, pela seção anterior, devemos ter
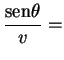 constante constante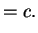 |
(5.1) |
Como 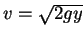 e
e 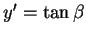 ,
combinando a identidade trigonométrica
,
combinando a identidade trigonométrica
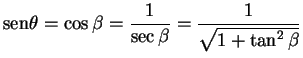 com (5.1) obtemos
com (5.1) obtemos
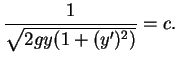 Simplificando esta última equação, chegamos a
Simplificando esta última equação, chegamos a
![$\displaystyle y\left[1+(y')^2\right]=k,$](img73.gif) |
(5.2) |
onde 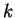 é uma constante positiva. Note a semelhança desta equação
com (2.5).
é uma constante positiva. Note a semelhança desta equação
com (2.5).
Não é nosso propósito resolver a equação
acima. Indicamos aos interessados a referência [S,
pag. 626,627, vol.1]. A propósito, James Bernoulli mostrou apenas
que a curva que solucionaria o problema da braquistócrona deveria
satisfazer a equação (5.2) cuja
solução já era conhecida naquela época. A solução
geral de (5.2) é dada na forma paramétrica
por
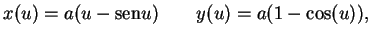 onde
onde 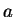 é uma constante que fica determinada de modo que a curva passe pelo
ponto B (veja figura ).
é uma constante que fica determinada de modo que a curva passe pelo
ponto B (veja figura ).
A curva dada pelas equações acima representa uma ciclóide
que é a mesma curva que se obtém quando um ponto fixado de
um círculo de raio 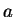 descreve quando este círculo rola sobre uma reta.
descreve quando este círculo rola sobre uma reta.
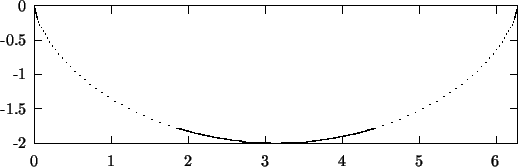
|
Figura 8: A ciclóide.
Esta curva possui várias propriedades interessantes mas nos restringiremos
a uma delas:
O tempo que uma partícula inicialmente em repouso leva para
percorrer um arco de ciclóide até o seu vértice mais
baixo independe da sua posição inicial. Na verdade, o
problema da curva tautócrona, ou seja, de se encontrar uma
curva com esta propriedade já havia sido resolvido, o que possibilitou
resolver a equação do problema da braquistócrona.


Next:Comparando
Com Outras CurvasUp:O
Problema da BraquistócronaPrevious:Refração
na Atmosfera Terrestre
2000-01-31


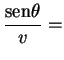 constante
constante![]() e
e ![]() ,
combinando a identidade trigonométrica
,
combinando a identidade trigonométrica
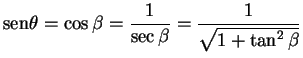
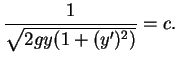
![]() é uma constante positiva. Note a semelhança desta equação
com (2.5).
é uma constante positiva. Note a semelhança desta equação
com (2.5).
![]() descreve quando este círculo rola sobre uma reta.
descreve quando este círculo rola sobre uma reta.
