![\includegraphics[width=3in,height=2in]{d:/braqui/part.eps}](img9.gif) |
Esquematizando no plano coordenado, temos:
![\includegraphics[width=3in,height=2in]{d:/braqui/part.eps}](img9.gif) |
Sabemos da Física que quando uma partícula atua sob a
ação da gravidade, o trabalho realizado para se deslocar
de ![]() até um ponto
até um ponto ![]() é igual à variação da energia cinética.
Assim, denotando por
é igual à variação da energia cinética.
Assim, denotando por![]() o módulo da velocidade (velocidade escalar) da partícula
no ponto
o módulo da velocidade (velocidade escalar) da partícula
no ponto ![]() por
por ![]() o seu deslocamento vertical e por
o seu deslocamento vertical e por ![]() a sua massa, temos
a sua massa, temos
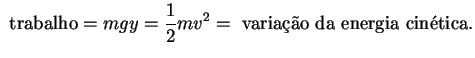 |
(2.1) |
Mas, a velocidade escalar é a variação do espaço
percorrido -- ![]() no esquema acima -- pelo tempo, ou seja,
no esquema acima -- pelo tempo, ou seja,
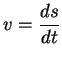 e, por (2.1),
e, por (2.1),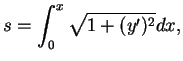
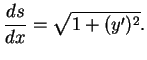
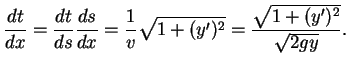
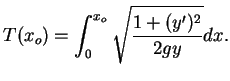 |
(2.2) |
O problema se resume a encontrar uma função ![]() que minimize o tempo acima e o procedimento usual para a sua resolução
é fazer uso do Cálculo Variacional. Mais precisamente, precisamos
encontrar uma função
que minimize o tempo acima e o procedimento usual para a sua resolução
é fazer uso do Cálculo Variacional. Mais precisamente, precisamos
encontrar uma função ![]() que satisfaça
que satisfaça
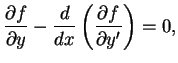 |
(2.3) |
onde
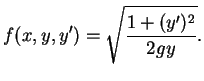 |
(2.4) |
Após alguns cálculos, combinando (2.3)
e (2.4)
o problema se resume a encontrar uma função ![]() que satisfaça
que satisfaça
![\begin{displaymath}\begin{cases}\frac{d}{dx}\left[\left(1+(y')^2\right)y\right]=0 y(0)=0, y(x_o)=y_o.\end{cases}\end{displaymath}](img31.gif) |
(2.5) |
Nós não utilizaremos este método geral para a resolução do problema. A resolução que apresentaremos a seguir segue os passos da resolução apresentada por James Bernoulli. Antes faremos um breve intercurso num problema de Óptica que, embora aparentemente não esteja relacionado ao problema da braquistócrona, se mostrará de grande valia para a sua resolução.