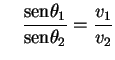

Next:Refração
na Atmosfera TerrestreUp:O
Problema da BraquistócronaPrevious:A
Modelagem do Problema
Um Problema de Refração
Consideremos um raio de luz que vai de 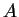 a
a 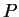 com velocidade constante igual a
com velocidade constante igual a 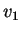 e segue de
e segue de 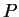 a
a 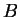 com velocidade constante
com velocidade constante 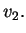
![\includegraphics[width=3in,height=2in]{d:/braqui/refra.eps}](img34.gif)
|
Figura 3: refração de um raio
de luz
Em geral, as velocidades acima são distintas e dependem do meio
em que a luz está se propagando. Por exemplo, quanto mais denso
o meio, mais lenta será a sua velocidade. Para fixar as idéias
podemos pensar no esquema acima que na parte superior o meio de propagação
da luz é o ar e na parte inferior a água. Como a água
é mais densa que o ar temos neste exemplo, 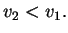 Se denotarmos por
Se denotarmos por 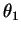 o ângulo agudo que o segmento
o ângulo agudo que o segmento 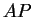 faz com a vertical e por
faz com a vertical e por 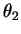 o ângulo agudo que o segmento
o ângulo agudo que o segmento 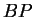 faz com a mesma vertical, é de se esperar que
faz com a mesma vertical, é de se esperar que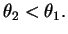 Este fato é uma conseqüência (verifique!) da lei da refração
de Snell:
Este fato é uma conseqüência (verifique!) da lei da refração
de Snell:
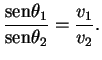 |
(3.1) |
Na verdade, a relação que fora descoberta empiricamente
por Snell em 1621 é que, fixados os dois meios por onde a luz se
propaga, tem-se que  é proporcional a
é proporcional a 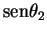 independentemente do ângulo de incidência do raio.
independentemente do ângulo de incidência do raio.
A primeira prova matemática de (3.1)
foi fornecida pelo matemático francês Pierre de Fermat e é
baseada no seguinte princípio que leva seu nome:
Princípio do Tempo Mínimo de Fermat A trajetória
real percorrida por um raio de luz de 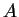 a
a 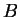 é a que minimiza o tempo total de percurso.
é a que minimiza o tempo total de percurso.
Passemos à demonstração de (3.1).
Lembrando que
tempo gasto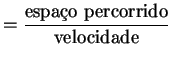 e fazendo uso do Teorema de Pitágoras, é fácil ver
que o tempo gasto para o raio de luz ir de
e fazendo uso do Teorema de Pitágoras, é fácil ver
que o tempo gasto para o raio de luz ir de 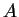 até
até 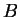 é dado por
é dado por
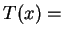 tempo
gasto de A a P
tempo
gasto de A a P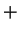 tempo
gasto de P a B
tempo
gasto de P a B
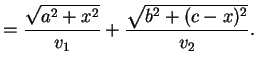 Assim, nosso problema está reduzido a achar
Assim, nosso problema está reduzido a achar 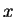 que minimize
que minimize 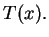 Note que este problema é bem mais simples do que aquele discutido
nas seções anteriores. Agora, se um tal ponto
Note que este problema é bem mais simples do que aquele discutido
nas seções anteriores. Agora, se um tal ponto 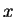 existir ele deve satisfazer
existir ele deve satisfazer 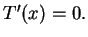 Calculando a derivada de
Calculando a derivada de 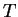 e achando as suas raízes, obtemos
e achando as suas raízes, obtemos
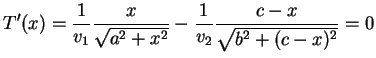
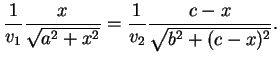 |
(3.2) |
Note que o ângulo 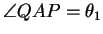 e, portanto,
e, portanto,
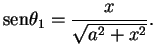 A partir do triângulo
A partir do triângulo 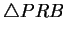 obtemos
obtemos
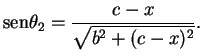 Combinando estes resultados com (3.2) chegamos
a
Combinando estes resultados com (3.2) chegamos
a
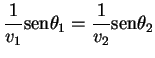 ou, simplesmente,
ou, simplesmente,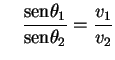 que é a relação procurada.
que é a relação procurada.


Next:Refração
na Atmosfera TerrestreUp:O
Problema da BraquistócronaPrevious:A
Modelagem do Problema
2000-01-31
![\includegraphics[width=3in,height=2in]{d:/braqui/refra.eps}](img34.gif)
![\includegraphics[width=3in,height=2in]{d:/braqui/refra.eps}](img34.gif)
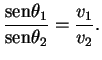
![]() é proporcional a
é proporcional a ![]() independentemente do ângulo de incidência do raio.
independentemente do ângulo de incidência do raio.
![]() a
a ![]() é a que minimiza o tempo total de percurso.
é a que minimiza o tempo total de percurso.
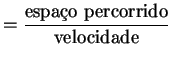
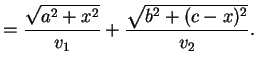
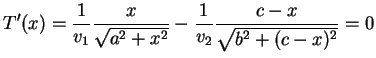
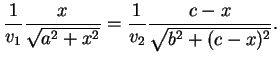
![]() e, portanto,
e, portanto,
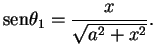
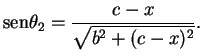
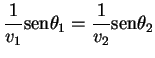 ou, simplesmente,
ou, simplesmente,